[프로그래머스]연속된 부분 수열의 합(lv.2) (kotlin)
이번에 푼 문제는 프로그래머스 LV2의 문제였다.
❔문제❔
이 문제에서는 어떤 수열과 k가 주어질 때 그 수열의 부분 수열 중 아래 조건을 만족하는 부분 수열을 찾아 출력해야 했다.
- 부분 수열의 합=k
- 합이 같은 부분 수열 이라면 길이가 짧은 것
- 합도 같고 길이도 같다면 시작 위치가 먼저인 것
처음에는 이걸 어떻게 구하지 싶어서 이것 저것 괜히 어렵게 생각했다가 다 실패했다ㅠㅠ
결국 Simple is Best의 정신으로 그냥 문제를 그대로 한번 구현해 보기로 했다.
🙌Solution🙌
〰️ 이중 for문을 통한 구현
fun solution(sequence: IntArray, k: Int): IntArray {
var answer: IntArray = intArrayOf()
sequence.indexOf(k).let{
if(it>0) return intArrayOf(it,it)
}
for( startIndex in 0 until sequence.size){
if(sequence[startIndex]>k)break
var sum=0
for(endIndex in startIndex until sequence.size){
if(sequence[endIndex]>k)break
sum+=sequence[endIndex]
if(sum==k) {
val subArr=intArrayOf(startIndex,endIndex)
if(answer.isEmpty())answer=subArr
else if(answer[1]-answer[0]>endIndex-startIndex)answer=subArr
else if(answer[1]-answer[0]>endIndex-startIndex&&answer[0]>startIndex)answer=subArr
break
}
else if(sum>k)break
}
}
return answer
}
위 코드는 중 for문으로 모든 부분수열을 검토하며 조건에 맞는 부분수열을 찾아내는 코드이다.
시간 복잡도는 $O(n^2)$!
비록 장렬하게 시간초과를 와다닥 먹어버렸지만(🥲) 그래도 역시 처음 접근은 담백하고 심플한게 좋은 것 같다.
코드가 돌아가긴 하므로 더 풀어나갈 자신감이 생겼다!👍
〰️ two pointer 알고리즘을 통한 접근
중간에 여러 우여곡절이 있었지만 어쨌든 시간복잡도를 줄이는 방법을 찾아냈다!
two point알고리즘을 사용하면 위의 시간복잡도를 $O(n)$으로 줄일 수 있다.
Two pointer 알고리즘
- 두 점의 위치를 저장하고 조건에 따라 변경해가며 범위를 조절
이 문제의 경우 두 점의 위치를 통해 부분 수열의 범위를 지정하고 원소의 합과 조건을 비교하며 범위를 조절하였다.
아래 코드는 다음과 같은 절차를 통해 동작한다.
- 반복문을 통해 prefixSum구하기
- prefixSum[n]은 sequence[0]~[n-1]까지의 합
-
따라서 sequence[5]~[8]인 부분 수열의 합은 prefixSum을 통해 아래와 같이 구할 수 있다.
sub=prefixSum[9]-prefixSum[5]
- prefixSum을 사용하여 부분수열의 합을 구하고 조건에 맞는 부분수열 찾기
- sum==k
- 조건을 검사하여 조건에 부합하면 answer에 저장
- startIndex를 올려 더 좁은 범위에서 탐색을 이어감
- sum>k
- 이 경우 sum을 줄이는 방법은 startIndex를 올리거나, endIndex를 낮춰 sum을 줄일 수 있다.
- 그러나 endIndex번째의 원소는 startIndex의 원소보다 항상 크므로 누락없이 탐색을 진행하기 위해 startIndex를 올려가며 범위를 좁혀야한다.
- sum<k
- 이경우 sum을 늘리는 방법은 위의 경우와 반대이다. (startIndex를 낮추거나, endIndex를 올림)
- 탐색이 startIndex를 늘려가는 방향으로 진행되고 있으므로 endIndex를 올려 범위를 조절한다.
- sum==k
- 수열의 범위 내에서 2를 반복
import kotlin.math.*
class Solution {
fun solution(sequence: IntArray, k: Int): IntArray {
var answer: IntArray = intArrayOf()
val prefixSum=IntArray(sequence.size+1){0}
val sub=mutableListOf<IntArray>()
sequence.indexOf(k).let{
if(it>0) return intArrayOf(it,it)
}
//prefixSum구하기
for(i in sequence.indices){
prefixSum[i+1]=prefixSum[i]+sequence[i]
}
//부분수열 구해가며 조건에 맞는거 찾기
var startIndex=0
var endIndex=0
while(endIndex<sequence.size){
var sum=prefixSum[endIndex+1]-prefixSum[startIndex]
if(sum==k){
if(answer.isEmpty())answer=intArrayOf(startIndex,endIndex)
else if(answer[1]-answer[0]>endIndex-startIndex)answer=intArrayOf(startIndex,endIndex)
else if(answer[1]-answer[0]==endIndex-startIndex&&answer[0]>startIndex) answer=intArrayOf(startIndex,endIndex)
startIndex++
}
else if(sum>k) startIndex++
else endIndex++
}
return answer
}
}
줄어든 반복 횟수 때문인지 이번에는 무사히 시간 내에 통과할 수 있었다.
알고리즘을 공부할수록 시간 복잡도의 중요성과 더불어 이중for문은 함부로 쓰지 않아야 하는 것을 뼈저리게 느낀다.🥲
🚀More
원래는 문제를 풀고 나면 항상 뭔가 성능 개선을 위한 advanced를 찾아내서 여기에 적었었는데 이번에는 advanced라고 하기는 성능이 안 좋아지는 방향으로의 생각이라서 more이라는 제목을 사용했다.
다른 블로그들을 찾아보니 이렇게 합을 구하는 부분수열 문제 말고 부분수열 자체를 구하는 문제에서는 DFS를 사용하여 탐색하는 방법도 있다고 해서 위 문제도 DFS를 사용해서 풀 수도 있겠다는 생각이 들었다.
물론 시간 복잡도는 $O(2^n)$일거라 위의 two point알고리즘을 사용한 것 보다 성능이 떨어지겠지만 그냥 한번 해보고 싶었다🤔
그렇지만 오늘은 이미 알고리즘 뇌를 너무 많이 썼기 때문에 오늘은 코드를 짤 수 없고 나중에 심심할 때 해보고 여기에 추가해 두려고 한다.😅
+)
나중에 찾을 때를 대비해서 개념만 간단히 써보면 부분수열은 아래와 같은 그림으로 표현할 수 있다.
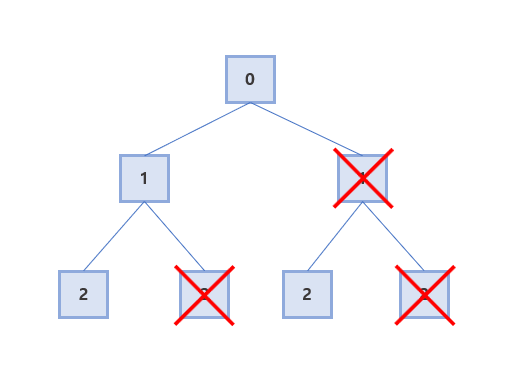
네모 안의 숫자가 수열의 인덱스라고 할 때 어떤 원소가 ‘포함되거나 포함되지 않거나’를 위와 같이 케이스로 나눠서 트리 형태로 만든다음에 DFS를 적용하자! 대충 이런 발상인 것 같다.

댓글남기기